12.6. Filtering
12.6. Filtering  12.6. Filtering
12.6. Filtering We need to sample the surfaces onto the screen in order to display the image. However we are not restricted to only sampling on point per pixel, as we did in the previous diagram. We can adopt a filtering process whereby each pixel is divided up into a number of sub-pixels. Sampling is carried out for these sub-pixels, and the resulting frequencies are combined in some way to produce a frequency for the pixel itself. This technique is the basis of filtering operations, and is called convolution. There are many different filtering methods, and we shall look at some of these.
The simplest approach is to average the frequencies of the sub-pixels to gain an overall frequency for the pixel. This method tends to be unsuitable for images with high levels of variation. An example application of this filter, known as the Box Filter, was seen in the section on Aliasing.
Crow (1981) notes that better results can be obtained by approximating a Bartlett filter. The pixel value is calculated from a weighted average of sub-pixels from inside and outside the domain of the pixel. The central sub-pixels are weighted more heavily than the outer ones.
He uses the example of row of 512 pixels being generated from a row of 1024 sub-pixels. Each pixel is generated from 9 sub-pixels, which form a 3x3 grid. Neighbouring pixels share a column of 3 sub-pixels. Naturally 3 rows of sub-pixels must be used to calculate one row of pixels. Where higher resolution sub-pixels are used, the number of sub-pixels per pixel will increase, for example forming a 5x5 or 7x7 grid.
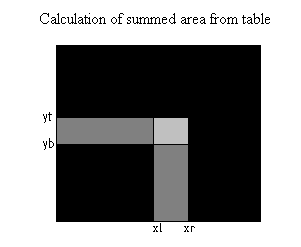
In the summed area technique, as described by Crow, (1984), texture intensities are replaced by the sum of intensities of all texels contained in the rectangle bounded by the texel of interest and the lower left corner of the image. Dividing the sum by the area of the rectangle gives the average intensity for the rectangle.