8.7. Octrees   

An octree is the natural progression from a quadtree for the representation of 3-D space. Rather than an area being divided into four, octrees divide a 3-D object space into eight smaller cubes known as cells. If any one of the resulting cells is homogeneous, that is the cell lies entirely inside or outside the object, the sub-division stops. If, on the other hand, the cell is heterogeneous, that is intersected by one or more of the object's bounding surfaces, the cell is sub-divided further into eight sub-cells. The sub-division process halts when all the leaf cells are homogeneous to some degree of accuracy (Carlbom and others 1985).

According to Samet (1990) the region octree is the simplest variant of the octree data structure. It also has the same drawbacks as the region quadtree inthe sense it is only an approximation of an image. The octree is also costly to compute because of the amount of data that must be examined.

Octrees have the same structure as a quadtree except that every parent node has eight children instead of the four used with octrees. Because of the eight children octrees are very useful in storing information about three-dimensional space. As you can see in the example the octree has exactly the same structure as a quadtree.  

    


   
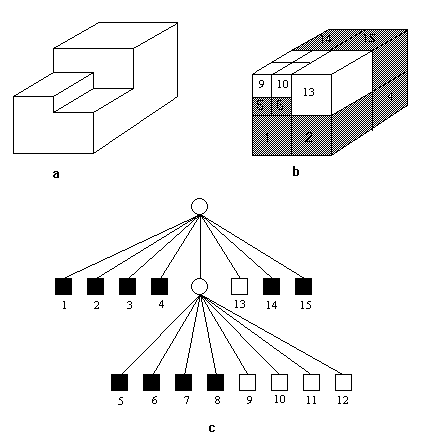
   Fig. 8.7 : 3-D image, its octree block composition and tree representation(Samet 1990)