8.5. Advantages of Quadtrees   

An advantage of quadtrees is that an image can be compactly represented. The compactness of the quadtree depends entirely on the image. An image with large areas of a single colour will become very compact, while an image that has a different colour for every pixel will yield no advantage at all. (Hunter and Stiglitz,1979)

Because of its advantages quadtrees have become very popular in GIS and spatial data representation. They are extremely useful for neighbourhood operations (Burroughs 1986). In GIS these include :

• comparing - ie. seeing if neighbouring cells are the same soil type.
• intersections - ie seeing if cells intersect.
• unions - ie combining cell together.

This makes quadtrees particularly useful in applications requiring images to be overlaid. They are also efficient for a number of image processing operations eg computing perimeters, labelling connected components, finding genus of an image, and computer centroids (Samet,1981).

There are also many algorithms available for the traversal and manipulation of trees in their many forms, and quadtrees can take full advantage of these. A rotation of 90 degrees anti- clockwise is achieved simply by moving each node as shown:

• North West -> South West
• North East -> North West
• South West -> South East
• South East -> North East

Burroughs (1986) and Samet (1990) also mention that quadtrees are useful in varying the resolution of an object. For example let us use the quadtree in figure 8.4 which represents the image in figure 8.1.a. If we want to vary the resolution on this image we can simply change all the grey nodes on level 1 to black nodes. This will produce the new image in figure 8.5.  

    


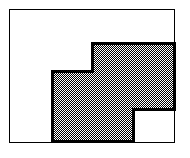
             Fig. 8.5 : Varied Resolution of Quadtree