8.3. Constructing a Quadtree
8.3. Constructing a Quadtree  8.3. Constructing a Quadtree
8.3. Constructing a Quadtree Before a quadtree can be constructed the image must be broken up into maximal blocks. Each quadrant of this image is then assigned one of the following values
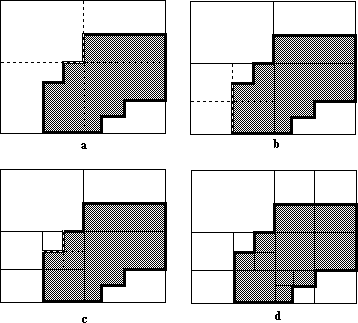
Fig. 8.3 : (a)first division (b)second division (c)third division (e)entire image divided
Enclosing figure 8.1a the image in a block produces the first level
of our quad tree. This can be seen in figure 8.4 where the entire square
is represented by Level 3. The square is then sub-divided into
four equal sized quadrants (hence the name quadtrees). This is
shown in figure 8.3a. In this particular case the NW quadrant is a white
square while all the rest of the quadrants are grey circles as
shown by level 2 in figure 8.4. The grey are again subdivided into
quadrants (in this example I have chosen to only use the SW
quadrant for simplicity sake). In figure 8.3b we see that the SW quadrant
now consists of 2 white, 1 black and a grey quadrant. This is
represented by the second group on level 1 of figure 8.4. The grey quadrant
is again subdivided. This is our final division because their
are no more greys left. We now have 1 white and 3 black
quadrants. This is, of course, done for the whole image. The
final quadtree can be seen in figure 8.4.

Fig. 8.4 : Final quadtree showing levels