8.2. Quadtrees
8.2. Quadtrees  8.2. Quadtrees
8.2. Quadtrees A quadtree is a hierarchical data structure used for image representation at the bit level. They encode images in terms of a tree structure and were initially designed to save storage by combining data which had identical or similar values.
According to Samet (1990), some definitions concerning two-dimensional data must be defined before looking at quadtrees. An image in two dimensions is an array of picture elements (pixels). If each pixel has only two states, black or white (on or off) then it is said to be binary. If it is possible to assign shades of grey then the image is said to be grey-scale (colour images have a similar principle to grey-scale). The more familiar quadtrees deal with binary images and so therefore we will deal primarily with binary images (The grey node mentioned later is not to be confused with grey-scale). It is also assumed that the background of all images is white.
Quadtrees define a hierarchical data structure whose common property is that they are based on the principle of recursive decomposition of space. There are several kinds of quadtrees based on different types of data. For example point data, areas, curves, surfaces and volumes all use different quadtrees. The most common type of quadtree, and the example that is being used, is known as a region quadtree (see figure 8.1, figure 8.3 and figure 8.4. examples of image, binary array, blocks and quadtrees).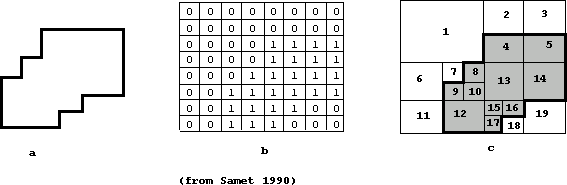
Fig. 8.1 : (a) a region (b) its binary array (c) maximal blocks
The image is broken down into sub-quadrants where each quadrant is represented by a node. The root node in effect, represents the entire image. The root node has four children nodes, each representing the four quadrants of the original image (labelled NW, NE, SW, SE - or the north-west quadrant, north-east quadrant, south-west quadrant, and south-east quadrant respectively). Each children node in turn has four children node associated with it, representing the sixteen sub-quadrants of the original image. The children of these sub-nodes in turn represent the sixty four quadrants of the image and so on, to form the resultant hierarchical quadtree.
When the quadtree is formed, the leaf nodes (the nodes representing each individual pixel of the image) represents the color of that pixel (eg black or white). If a non-leaf node has a mixture of non-uniform colored children nodes, it is represented by a 'grey' node. If a non-leaf node has all uniformly colored children nodes only, it is represented by the color of its children nodes. Its children nodes are then disregarded from the tree. Thus as can be seen, entire tree structure of nodes can be disregarded if the image has large uniformly colored regions.
As supported by Samet and Tamminen (1985), quadtrees and its variants have been
found to be useful in applications such as image processing,
computer graphics, pattern recognition, robotics, and
cartography.
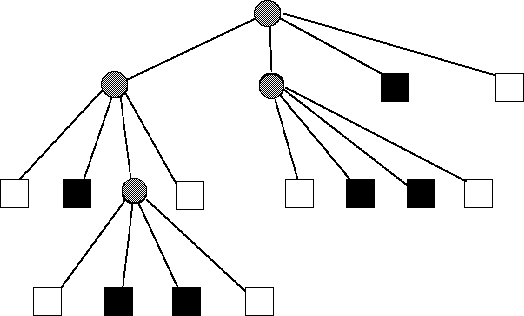
Fig. 8.2 : quadtree decomposition