4.4. Homogeneous Co-ordinate System.   

This system represents a point (x,y,z) in 3-D using 4-D co- ordinates: 

 

                          i.e.   [Wx, Wy, Wz, W ]

where W is a scale factor. [x,y,z,1] => scale factor is 1 
 

              [4,6,10,2] ==  [6,9,15,3] ==   [2,3,5,1]

Therefore many points in H.C.Space are (x,y,z) 


H.C.S  can be useful in Transformations:


Therefore Transformation is applied and resulting vector is converted into the Z=D plane with a scale factor of 1.


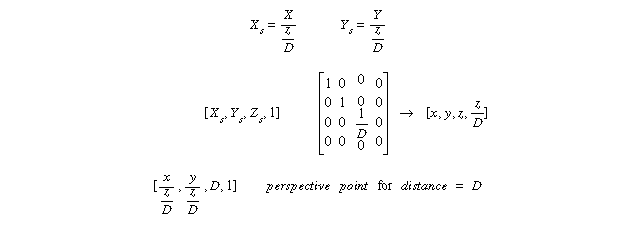
Other 3-D projections exist: 


ignore the z commponent                       L = length of viewed unit cube

                                               = angle of projection

Viewing an object rarely has the property of having ones eye at z = x = y = 0!
Nor is it likely that the object is sitting on the x = z plane.
We need to develop routines for arbitrary viewing of an object. 

Develop algorithms for manipulation of object with eye at origin, etc AND

also routines for transforming an object from some arbitrary 3-D coords

into the origin framework.


Where is object?            Xobj, Yobj, Zobj

Where is the screen?        Defined by View reference point  Vrpx, Vrpy, Vrpz


Where is plane normal?      ie what orientation is the screen?

       View plane Normal:    Vpnx, Vpny, Vpnz


What is size of view plane?

Window size ?

Where is eye?                Copx, Copy, Copz


What is orientation of eye?  Vupx,    Vupy,   Vupz

(Read section 8.3 in Van Dan & Foley first edition 8.4.2 " " " )

The transformation of an object requires: 


       translation of object s.t. COP is at origin ]

       rotation so that VPN is down -ve z axis     ] now as before with S & D

       rotation so that VUP is up   +ve y axis     ]

       change from World to viewing : exchange z axis

       Shear so centred

       Scale to fit view volume


  Transformpers  = Tper. Ry . Rx . Rz . Trl . Sh. Sper

          plus clipping.