4.2. Projections.   

Mapping 3-D co-ordinates to a 2-D screen => some kind of transformation. If we only use the (x,y) of (x,y,z) then this is an orthographic projection. Not realistic.  

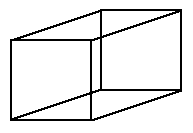
proj1.eps 

Orthographic projection is one of the parallel projections.  The other is

oblique.  The relative length information is still preserved but angles are not.

For the parallel projections the centre of projection is at infinity i.e the rays forming the object are parallel. If the Centre of Projection (C.O.P) is not at infinity then the projection is a perspective projection. 

For  // projection => direction of projection.

For perspective projection => C.O.P.