12.6. 2-D Geometry   

Lines
(1) ay=bx+c is equation of any straight line.
b/a is tangent of angle that line makes with positive x-axis.

    


   
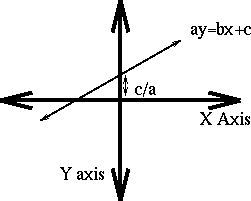
             Fig. 12.5 : Geometry illustration.

 if b=0, tangent is 0 and hence y = const.

 if a=0, tangent is infinite and line is x = const.

 and c/a (if finite) is the intercept of line on y-axis.

 if infinite then line // to y axis.

     p1 =(x1 ,y1 )

     p2 =(x2 ,y2 )

Therefore p=(x,y) can be given as


         (1-  )p1 +  p2 for some real  .


         =((1-  )x1 +  x2 ,  (1-  )y1 +  y2 )


               where if 0<=  <=1 then p lies between p1 and p2

           = ( distance of p -> p1 ) / ( distance of p2 -> p1)

Example:

Calculate point of intersection p = (x,y) of two lines joining:


                p1 =(x1 ,y1 ) -> p2 =(x2 ,y2 )

  and          p3 =(x3 ,y3 ) -> p4 =(x4 ,y4 )


 General point p =

                        (1) (1- )p1 +  p2

                        (2) (1- )p3 +  p4

                 since P is on both lines.


              (1- )p1 +  p2 = (1-  )p3 +  p4 = p

=>              (1- )x1 +  x2 = (1-  )x3 +  x4

and            (1- )y1 +  y2 = (1-  )y3 +  y4


=>               (x2 - x1 ) +  (x3 - x4 ) = x3 - x1

and             (y2 - y1 ) +  (y3 - y4 ) = y3 - y1


2-equations -2 unknowns ---> soluble.

Set       = (x2 - x1 )(y3 - y4 ) - (x3 - x4 )(y2 - y1 )

=>        = { (x3 - x1 )(y3 - y4 )- (x3 - x4 )(y3 - y1 ) } /

       subprogram intercept (x1,y1,x2,y2,x3,y3,x4,y4,X,Y:real)

       local real psi,phi;


              psi  (x1-x2)*(y4-y3)-(y1-y2)*(x4-x3);

              if (abs(psi)<0.00001) then {lines are //}

              else

              begin

                phi  ((X3-X1)*(Y3-Y4)-(X3-X4)*(Y3-Y1))/psi;

                X  (1-phi)*X1+phi*X2;

                Y  (1-phi)*Y1+phi*Y2;

              endif;

              return;


       end_subprogram.