12.5. 2-d Geometry - revision.   

Let P be the point (x₁ ,y₁ ) and Q be the point (x₂ ,y₂ ) then the length of vector PQ is

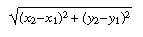
and its slope is

Lines are parallel if the two slopes are equal. i.e if m1=m2.
Lines are perpendicular if the two slopes when multiplied together equal -1. i.e m1*m2 = -1.

The equation of a line through P with slope m is

          y- y1 = m(x- x1 )


This leads to the general equation for a line

                ax + by +c =0


The equation of a circle with radius r and centre the origin is given by:

                x2 + y2 = r2

The equation:

                x2 +y2 + 2ax + 2by + c = 0

represents a circle with centre (-a,-b) and radius

                sqrt ( a2 + b2 - c )


For converting between Cartesian and Polar co-ordinates remember

that:

               x =  r cos(  )         y =  r sin(  )

               r= sqrt ( x2 + y2 )    tan(  ) = y / x


And for analysis of triangular regions remember that for any

triangle ABC:

             a/sin(A)  = b/sin(B) = c/sin(C)

 and

           area = 0.5 ab sin(C) = sqrt( (s- a)(s- b)(s- c)s )


where s= 0.5(a+b+c)


 and

                 cos(A) = ( (b2 + c2 - a2) ) / 2bc

    


   
     Fig. 12.3 : Further examples of ill-treated circles.

    


   
   Fig. 12.4 : Still further examples of ill-treated circles.

When constructing circles or parts thereof remember that:


 a circle is just an arc carried through 360 degrees

 For an arc at radius r, subtending an angle theta at centre


 length of arc = r*          length of chord = 2r sin(  /2)

 area of sector= 1/2 r2*    area of segment = 1/2 r2 (  -sin(  ))


A good reference book to brush up on 2-D geometry is the Schaums

outline series on Analytical Geometry by Joseph H. Kindle. This

has been put in closed reserve for your use. Chapters 1, 2, 3,

4, 8, 9, and 10 should be read (quickly) if need be.